Aerodynamics of Dragon Flight

There is a better presentation of dragon aerodynamics, which I gave at the Livermore Library in December 2022.  A recording of the talk is at https://www.youtube.com/watch?v=ASpntEpOqpk.

Ever wonder if dragons can really fly? This post presents a quantitative analysis of the possibility of large flying dragons, up to the size of a humpback whale.

One of my goals while writing Dragon’s Ridge was to portray dragon flights realistically. As an aerospace engineer, I have the tools to ensure this, and I saw an opportunity educate the readers while telling the story.

For the impatient

A 300-pound (136 kg) creature with a 30-ft (9-meter) wingspan and a 5-ft (1.5-m) chord (the from leading edge to trailing edge) can reasonably cruise at a speed of 40 mph (65 kph). Taking off may push the limits, but it’s plausible.

A warning before you read on

This analysis is a bit like calculating whether Santa Claus can actually visit all the world’s good kids’ residences in 24 hours. If you’d prefer to think that a dragon the size of a T-Rex or a whale can fly, maybe you should stop reading now.

What does it take for a dragon to fly?

A wing’s geometry determines how “lifty” it is. Engineers characterize this by the lift coefficient, $C_L$. Speed helps too. The faster you go, the less lifty the wing has to be. This graph shows the coefficients needed to keep representative creatures aloft, depending on its weight and speed:

In the figure’s legend, Pyramine refers to a 300-lb dragon in Dragon’s Ridge. Ashwing is a 700-lb dragon. Other lines represent dragons of the same design but different size. The sizes shown correspond to the weights of a golden eagle, the two dragons, a clydesdale (big horse), a white rhino (5 feet tall at the shoulders), a T-Rex and a humpback whale, listed in increasing order. The presumed weights are in the appendix at the end of this post. I’ll refer to the animals because I think that’s easier imagine than, “a 1800-lb dragon.”

The y-axis is a log scale. Each grid line is a 10-fold increase. It tops out at 10, but the maximum realistic value for $C_L$ is about 3. Modern airliners have $C_L\approx2$ on take off and 3 on landing. They change their $C_L$ by deploying flaps to change their wing shapes. Dragons and bats may do the same, by flexing their spiny wing fingers, something that birds can’t do. Pitch also affects liftiness, a fact well known to children who’ve held their hand out the window of a moving car. The practical maximum $C_L$ is around 3, however you do it.

Cruising at 40 mph (65 kph), Pyramine requires a $C_L=0.5$, a reasonable value. Ashwing has to fly at 61 mph (98 kph) or shape its wings to get a higher $C_L$. In fact, any dragon can fly if it attains enough airspeed. Lots of speed in some cases. Let’s see how they might get that speed.

Most birds spring into the air with their legs. Others, like the albatross run along the ground, looking kind of silly before it gets airborne and turns into a graceful flyer. Larger bodies don’t spring as well. That’s why power lifters don’t make good sprinters. Dragons can hypothetically jump off cliffs to gain speed, but relying solely on that would get them in trouble if they ever end up on flat ground.

For take-off, let’s use the take-off coefficient of airliners, $C_L=2$. It’s not great for sustained flight, but okay for take-off. Pyramine can take off at 20 mph. Ashwing at 31 mph, and so forth, as shown in this table.

	Pyramine	Ashwing	Clydesdale	Rhino	T-Rex
T/O speed (mph)	20	31	49	86	141
“Spring” time (s)	0.6	0.8	1.1	1.6	2.2
G’s pulled	1.8	2.0	2.3	2.7	3.1
Drag (pounds)	34	140	660	4200	22500

“Spring” time is how long it takes the dragon to spring into the air to reach the take-off speed. I gave Pyramine 0.6 seconds and scaled it up for the bigger dragons’ longer limbs. The third row shows how many G’s they’d have to push with. One G is just the creature’s weight. A T-Rex-sized dragon has to sustain 2.1 more times its weight. Imagine the dragon squatting with two similar dragons sitting on its shoulders. If it can’t do this, I think it’d have to take off albatross-style.

The table’s last row is aerodynamic drag at the take-off configuration. It’s very high for the big dragons, which brings us to the next question.

Can a dragon stay airborne?

To maintain speed, anything that flies has to overcome aerodynamic drag. This graph shows how much drag there is on our various-sized dragon:

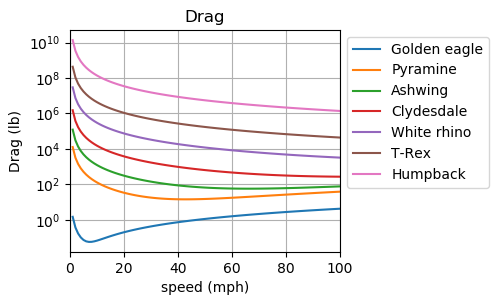
Interestingly, drag is lowest a certain speed that depends on the dragon’s weight. Once the dragon is airborne it will want to reach this speed to fly efficiently. This is about 7.5 mph for the eagle-sized dragon, car speeds for Pyramine and Ashwing and airplane speeds for the rest. I’ve plotted the drag on a log scale, so even a small change in the line makes a significant difference. Drag at the efficient speed is about an ounce for the eagle-sized, 15 pounds for Pyramine, 60 lbs for Ashwing. The clydesdale-sized dragon has to fight 270 lbs of drag at minimum. I suppose that’s like flying while pulling a plow. This is the best case, the lowest drag.

At the take-off speed I computed above, drag is much worse. At take-off speed, the rhino-sized dragon experiences drag three-quarters its weight. It could avoid this by leaping with more power to take off at a higher speed, but doing zero to 86 mph in 1.6 seconds already is implausible, so a flying rhino-sized (or bigger) dragon is out. For T-Rex and humpback, take-off drag is more than their weights.

More interesting than drag is the energy expended to overcome it. Here is how much energy a dragon requires for, say, a 62-mile hunting trip:

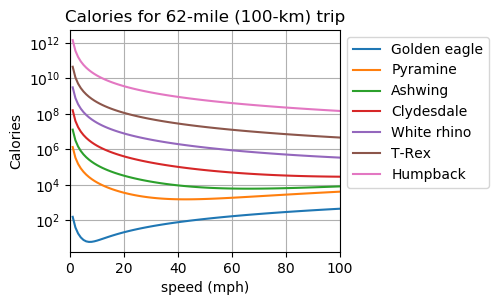
Flying at their most efficient speed for 100 km, this is how many calories the dragons burn:

Weight	Pyramine	Ashwing	Clydesdale	Rhino	T-Rex
Calories	1500	6000	28K	170K	900K

Burning hundreds of thousands of calories in search of food seems like a sure way to starve to death. And by the way, the T-Rex-sized dragon has to fly at 300 mph, so it finishes the trip and burns almost a million calories in 12 minutes.

Where does the drag come from?

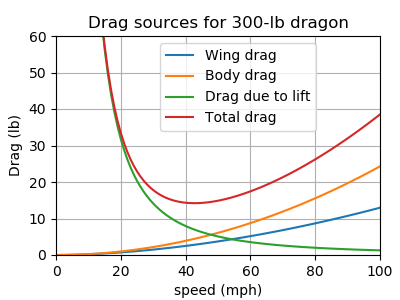
In case you were wondering, I broke down drag into 3 components: the dragon’s body, its wings and something called “drag due to lift”. The third one is caused by using a large $C_L$. This is why airplanes don’t fly in the take-off or landing configuration, even though they can generate big $C_L$’s. Drag from the body and wings go up with speed, but drag due to lift goes down. The sum is U-shaped.

What I didn’t mention

The purpose of this post is for fun, to make you think about realistic dragons and maybe to show how cool science and engineering is. To keep it simple, I didn’t consider some things, such as:

Large dragons need large wings to fly, but large wings lead to structural difficulties. I didn’t consider stress on the dragon’s bones, joints and tendons, or whether the they are strong enough.

Smart dragons don’t just rely on their wings. They’d take advantage of wind and thermals like large birds do. (Of course, if they drop faster than the air mass is rising…)

Ground effect reduces drag, which is particularly helpful for getting well past the inefficient take-off speed.

The analysis I used was developed for airplanes, rigid bodies propelled through the air by engines. Birds and dragons propel themselves by flapping their wings. I’ve seen some research using computer simulations to analyze flapping wings, and it’s much more complex than airplane aerodynamics. I assumed that the results would be comparable, at least in a steady cruise. At the extreme low end of speed range, like near hovering, a different mechanism is used for lift, far from the steady flows airplanes experiece.

Appendix 1: Animals of representative weights

I used animals to represent dragon weights. Here are the weights I actually used in the calculations:

Ashwing700318Clydesdale1800820

Key name	Weight
	Pounds	Kg
Golden eagle	10	4.5
Pyramine	300	136
White rhino	5500	2500
T-Rex	15000	6800
Humpback whale	55000	25000

And here are the dragons sizes, roughly scaled to those weights:

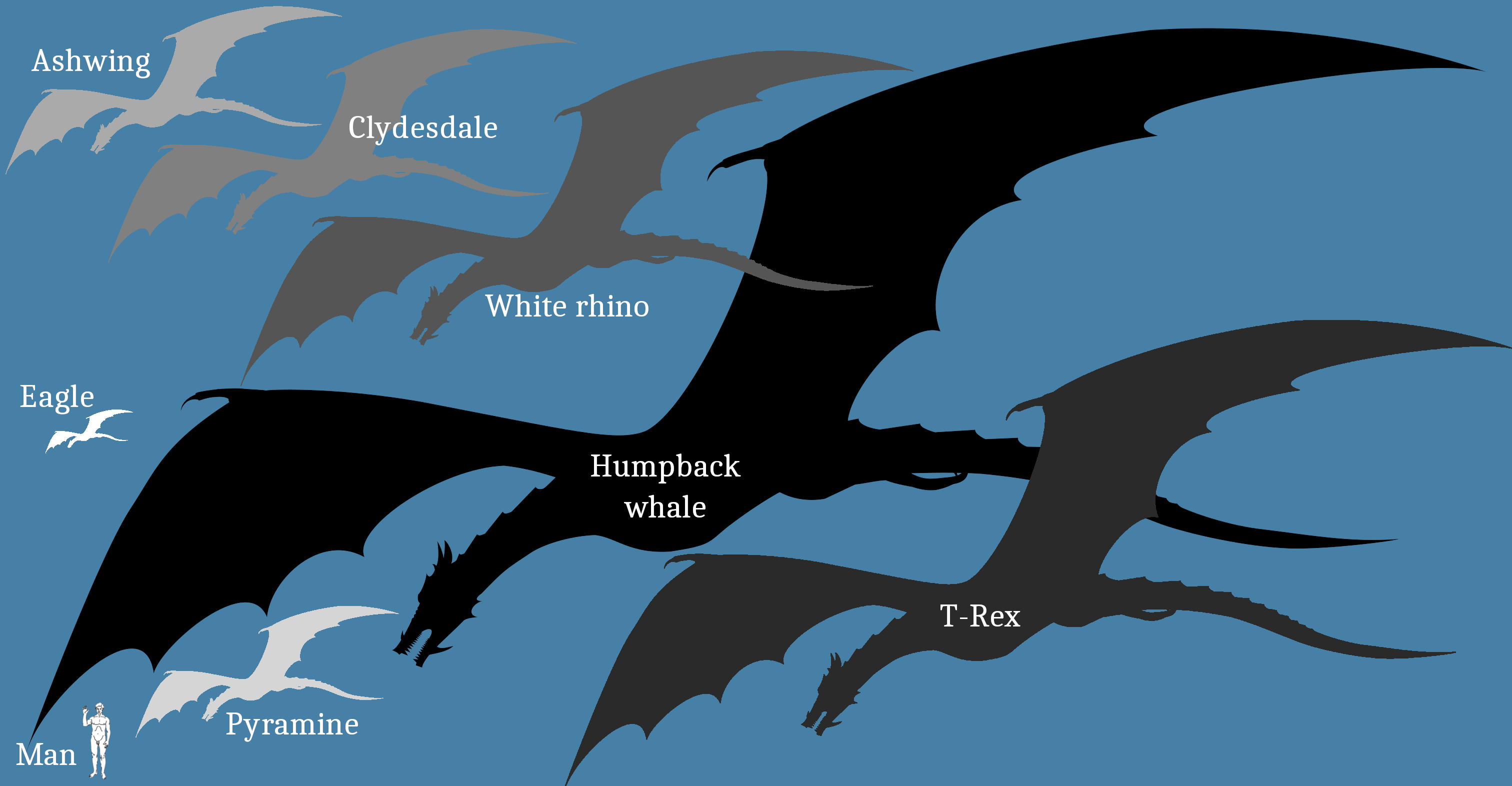
In the opening scene, I described the dragon as about the size of a yearling horse. The dragon could conceivably weigh less because its composition is somewhat lighter. Carrying Isodore, it would weigh around 400 pounds.

Appendix 2: Equations of aerodynamics

If you’re interested in how I got the numbers, here are the equations I used. I learned them in an upper-division aerospace engineering class and a graduate level course on viscous flow. The hard calculus and engineering analysis lead to these relatively simple algebraic relationships.

Lift:
$$L = q C_L A$$
$$q = \frac{1}{2} \rho V^2$$
where $\rho$ is the air density, $V$ is airspeed, $A$ is wing area. $q$ is dynamic pressure, the same dynamic pressure they talk about when launching a rocket. Drag:
$$D = D_b + D_w + D_L$$
the sum of drag from the body, the wing friction and drag due to lift.
Body drag:
$$D_b = q C_{D,b} \pi r^2$$
I used the drag for a sphere, $C_{D,b}=0.25$, the size of the dragon’s chest, with radius $r$. The dragon is sleeker in shape but more aerodynamically dirty (from the head, legs and surface bumps), so assuming they kind of balance out in the end. Wing friction drag:
$$D_w = 2 q C_f A$$
Turbulent friction coefficient
$$C_f = \frac{0.074}{Re_c^{1/5}}$$
Reynold’s number based on wing chord $c$
$$Re_c = \frac{\rho V c}{\mu}$$
where $\mu$ is the air viscosity. Drag due to lift:
$$D_L = q C_{D,L} A$$
$$C_{D,L} = \frac{C_L^2}{\pi R}$$
where $R$ is the wing aspect ratio, the ratio of wing span to wing chord. This assumes a elliptical wing or a reasonably tapered one, like the WWII fighers’. It would be worse for paddle-shaped wings, which are basically tapered the wrong way.